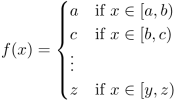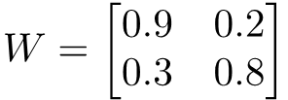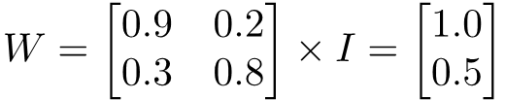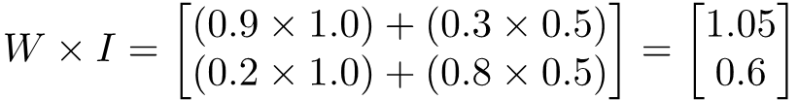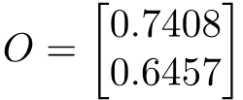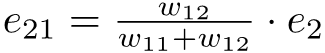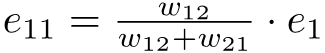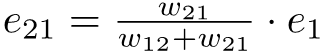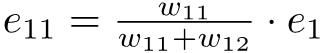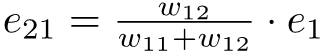Create Your Own Neural Network From The Scratch (A.I - 101)

[Kuchwizzy]

Part 05 - Neurons, Nature’s Computing Machines​

Kompyuta ina uwezo mkubwa wa kupiga mahesabu kwa kasi (computing power), richa ya nguvu hii, kompyuta aina uwezo wa kufanya majukumu magumu kama yanayofanywa na ubongo wa viumbe hai hata kidogo kama njiwa

Uwezo kama wa kutafuta chakula, kujenga kiota au kukimbia hatari, haya yote ni majukumu magumu sana lakini hufanywa kwa urahisi sana na ubongo wa njiwa ambao una computing power ndogo ukilinganisha na kompyuta inayoundwa na mabilioni ya vifaa vya kieletroniki

Baada ya watafiti kuumiza kichwa kwa mda mrefu, ikagundulika kua tofauti ipo katika muundo wa kompyuta na ubongo wa viumbe hai (architectural difference)

Kompyuta inachakata data au kupiga mahesabu hatua kwa hatua (sequentially) na hakuna bahati nasibu kwenye mahesabu ya kompyuta (fuzziness), kila kitu kipo bayana

Wakati ubongo wenyewe unapiga mahesabu mengi kwa wakati mmoja (parallel) na kuna bahati nasibu kwenye mahesabu yake (fuzziness) kuna hatua hazipo bayana, hii tabia inafanya ubongo uweze kutatua tatizo katika situation ambayo jawabu halipo wazi.


Hii tofauti ya utendaji kazi ndio inayofanya ubongo uweze kutatua matatizo magumu zaidi (complex tasks) ukilinganisha na kompyuta.

Tutazame basic computing unit ya ubongo, Neuron

Neuron ni aina ya seli (cell) inayochukua taarifa (signal) kutoka kwenye mwili na kupeleka kwenye ubongo, na kutoa taarifa kwenye ubongo na kurudisha kwenye mwili

Neurons zote, bila kujali fomu zake, husafirisha taarifa za kiumeme (electrical signal) kutoka sehemu moja kwenye nyingine, taarifa huanzia kwenye dendrite, hupita kwenye axon mpaka kwenye terminals na kusafirisha zao la hio taarifa (output) kama input kwenda kwenye neuron inayofatia


Hivi ndio ubongo wako unavyoweza hisi sauti, mwanga, mguso na taarifa nyingine zote, taarifa kutoka sehemu zote na mwili wako husafirishwa na neurons za mfumo wako wa fahamu (nervous system) kwenda kwenye ubongo wako ambao nao pia umeundwa na neurons


Tunahitaji neurons ngapi kufanya majukumu magumu? ubongo wa binadamu umeundwa na neurons takribani bilioni 100, ubongo wa nzi una neurons takribani 100,000 lakini nzi anaweza fanya majukumu magumu zaidi kuliko kompyuta
Neurons 100,000 tunaweza kuzi replicate kwenye kompyuta

Kwahio siri ya ubongo ni nini? licha ya kuundwa na computing components chache zenye speed ndogo ya mahesabu, ubongo unauwezo wa kufanya complex tasks kuliko kompyuta

Siri ipo kwenye utendaji kazi wa neuron, hivyo tutazame jinsi gani neurons zinafanya kazi

Neuron zinapokea taarifa za kiumeme (electrical input) na kutoa taarifa nyingine ya kiumeme (another electrical output)
Kwa mtindo huu, inafanana kabisa na simple predictor au classifier tuliyo deal nayo hapo awali?

Je, tunaweza model neuron kama linear function ( y = Ax + B)?

Wazo zuri, lakini hapana, output ya neuron hai obey linear function

Ushahidi umethibitisha kuwa, neuron hazi react papo kwa papo, bali husubiria mpaka pale taarifa inapokua na nguvu zaidi kisha neuron ndio huzalisha taarifa nyingine kama output


Ni kama kujaza maji kwenye kikombe, maji humwagika tu pale kikombe kinapojaa mpaka juu

Hii tabia ya neuron ku suppress signal mpaka inapovuka kiwango fulani (threshold) ina-make sense, tabia hii inaiwezesha neuron ku ignore tiny au noisy signal (taarifa zisizo na maana yoyote) na kupitisha tu zile taarifa zenye nguvu au za maana.

Tuone kama hesabu inaweza kutusaidia ku model aina hii ya tabia, mathematically

Function inayochukua input naku generate output huku ikizingatia aina fulani ya kiwango, threshold hujulikana kama activation function
Kwenye hesabu, kuna activation functions nyingi za namna hii, step function rahisi ina tabia kama hii

Mfano:

Kwa values ndogo za input, x (ndogo kuliko 2) output ni low (0), lakini output ita jump kwa high values of x (kubwa kuliko au sawa na 2)

Ku model hii tabia ya neuron kwa usahihi zaidi tunaweza tumia aina nyingine ya activation function ukiacha step function
Sababu ya kuachana na step function ni kwamba, kuna sudden jump ya output pale threshold inapofikiwa, lakini kwenye neuron kuna gradual or smooth jump kuelekea threshold inapofikiwa

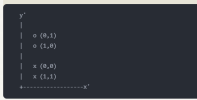
Tunaweza chagua aina nyingine ya activation function, inayojulikana kama sigmoid function au Logistic function inayotengeneza S-shaped curve

e ni mathematical constant inayojulikana kama Euler number yenye thamani ya 2.71828 (kwa kukadiria kwa sababu haina mwisho, ni transcendental number)

Hili ni umbo la grafu ya sigmoid function

Sababu nyingine ya kuchagua Sigmoid function kama activation function ni kwasababu ni rahisi kufanya nayo mahesabu, pia output ya sigmoid function ina range between 0 to 1 hivyo ni rahisi ku model probability / classification pia

Biological neuron inaweza chukua inputs zaidi ya moja, sio moja tu,, tumeona hili pia wakati tuna deal na Boolean functions
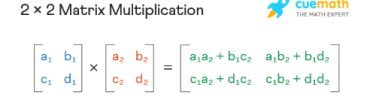
Kwahio tuna deal vipi na inputs zaidi ya moja? Tunazijumlisha tu zote kisha tuna apply sigmoid function kwenye resultant sum

Kama combined signals hazitoa kua na nguvu ( kama resultant sum haitokua higher than threshold) sigmoid function itazi suppress (output itakua 0) kama biological neuron inavyofanya. na kama combined signals zina nguvu, neuron ita react (fire), hii tabia inatupa sense of fuzziness tunayoitaka kwenye mahesabu yetu na tumeweza ku introduce non linearity kwasababu input ya activation function hai directly proportion to its output (hence, non-linear)

NB: Hapa unapaswa kutambua kua kwenye A.I tuna deal na abstract concepts za hesabu, artificial neuron au neural network ni equations tu za hesabu sio physical things ndani ya kompyuta, hapa neuron ni simple sigmoid function inayopokea inputs kutoka kwenye neurons nyingine na kutuma outputs kama inputs kwenda kwenye neurons nyingine ambazo pia ni sigmoid function au activation function yoyote utakayoamua kutumia.

Ni useful and powerful mathematical abstractions

Kila neuron, imeungana na neuron nyingine na kwa pamoja zinaunda mtandao wa neurons ama neural networks
(hence the name)

Utaona hapo kua, kila neuron inachukua inputs kutoka kwenye neurons nyingi zilizopita na kutuma outputs, kama inputs kwenda kwa neurons nyingi zinazofatia

Ku model hii tabia, tunapaswa kuwa na network ya neurons ambapo kila neuron imeungana na neurons nyingine

Unaweza kujiuliza, ni sehemu gani ya mtandao wa neva (neural network) unajifunza? ipi ni parameter au variable tunayoweza kui adjust ili kupata correct outputs kama ilivyokua kwa simple predictor au classifier?

Jibu rahisi ni mahusiano au connection kati ya neuron moja na nyingine
Ukubwa wa mahusiano kati ya neuron na neuron hujulikana kama weight
Tunachofanya kwenye training ni ku adjust strength of connections au weights baina ya neurons

Jina lingine la neuron ni node
Tugusie kuhusu notation kidogo, w 2,3 ni weight (strength of connection) kati ya neuron au node ya pili kwenye tabaka (layer) ya kwanza na neuron au node ya tatu kwenye layer inayofata (ya kati)

Unaweza kujiuliza kwanini tumeamua ku connect hizi neurons kwenye mtindo huu wakati kuna mitindo mingi ya ku connect hizi neurons

Jibu ni kwamba mtindo huu ni simple encode kama computer instructions au code, na wakati wa training
Network yenyewe inachagua ni kwa namna gani i connect neurons kwa ku emphasize baadhi ya connections au weights na ku de-emphasize nyingine

Tunaweza kutumia mda huu ku formalize yote tuliyojifunza mpaka sasa

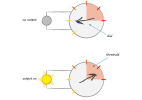
Biological Neurons and Their Efficiency​

Biological neurons can perform complex tasks with relatively slow speeds and few resources compared to computers due to several factors:

1. Massive Parallelism: Biological neurons operate in a highly parallel manner. The human brain has approximately 86 billion neurons, each connected to thousands of other neurons, allowing for simultaneous processing of vast amounts of information.
2. Adaptability and Plasticity: Biological neurons exhibit plasticity, meaning they can change their strength and structure in response to learning and experience. This adaptability allows the brain to optimize its processing capabilities efficiently.

Definitions​

Neuron​

A neuron is a nerve cell that is the fundamental building block of the nervous system. Neurons receive, process, and transmit information through electrical and chemical signals. In the context of artificial neural networks, a neuron is a computational unit that receives inputs, processes them through a function, and produces an output.

Activation Function​

An activation function in a neural network is a mathematical function applied to the input signal of a neuron to produce an output signal. It introduces non-linearity into the network, enabling it to learn and model complex patterns. Common activation functions include the sigmoid function, ReLU (Rectified Linear Unit), and tanh (hyperbolic tangent).

Sigmoid Function​

The sigmoid function is a type of activation function defined by the equation:

It maps input values to an output range between 0 and 1, making it useful for binary classification tasks. The sigmoid function has a smooth gradient, which helps in gradient-based optimization.

Weight​

In a neural network, a weight is a parameter that adjusts the input signal to a neuron. Weights are learned during the training process and determine the strength and direction of the input signal's influence on the neuron's output. Mathematically, weights are multiplied by input values and summed up before applying the activation function.
NB: Imagine each connection as a "wire" carrying a signal, and the weight determines the strength of that signal.

Node​

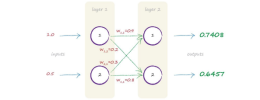
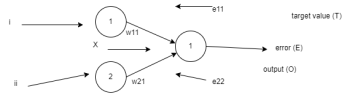
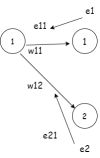
A node in a neural network, also known as a neuron or unit, is a basic processing element that receives inputs, applies a weight to each input, sums them up, and passes the result through an activation function to produce an output.

Example​

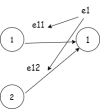
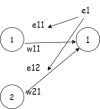
Here's a visual example of a simple neural network with definitions:

• Neuron (Node): Each circle in the network diagram represents a neuron.
• Weight (w): Each arrow connecting the neurons has an associated weight.
• Activation Function: The function applied at each neuron to produce an output. For instance, a sigmoid function can be used.
• Sigmoid Function:
  

Overall, biological neurons' ability to perform complex tasks efficiently and with minimal resources highlights the sophistication of natural neural processing, while artificial neural networks strive to emulate these principles using computational models.


Next : Following Signals Through A Neural Network

 

[Kuchwizzy]

Part 06 - Following Signals Through A Neural Network​

Hapo nyuma tumeona muundo wa Neural Network wenye matabaka (layers) tatu za neurons, huku kila neuron ikiwa imeunganishwa na neuron nyingine kutoka kwenye tabaka la nyuma na tabaka la mbele (previous and next layer)

Sasa tu visualize jinsi gani taarifa (signal) zinasafiri kwenye huu mtandao wa neurons (Neural Network)

Tuchukue neural network rahisi yenye layers mbili, kila layer ikiwa na neurons mbili.

Tu imagine kuwa, hizo inputs mbili zina thamani ya 1.0 na 0.5 ..

Vipi kuhusu weights ? Tunaweza anza na random values za weights (unakumbuka hii mbinu tuliitumia sana ku initialize values za constant c, na slope ya classifier A)

w1,1 ni weight kati ya neuron au node ya kwanza ya first layer na node ya kwanza ya second layer
w2,1 ni weight kati ya node ya pili kwenye first layer na node ya kwanza kwenye second layer

Vile vile
w1,2 ni weight kati ya node ya kwanza kwenye first layer na node ya pili kwenye second layer
w2,2 ni weight kati ya node ya pili ya first layer na node ya pili ya second layer
Tuseme kwa bahati nasibu tu w1,1 = 0.9, w2,1 = 0.3, w1,2 = 0.2 na w2,2 = 0.8

Tupige hesabu, kwa urahisi tuanze kukokotoa output ya kila neuron

First layer au kwa jina lingine input layer kazi yake ni kupokea training data au raw data kwa jina lingine
Neuron au node za hii layer ya kwanza ya neural network hazi paswi ku apply activation function

Kuna sababu mbili kuu nyuma ya huu uamuzi (design decision)

1. Hakuna chochote cha kujifunza kwenye layer hii ya kwanza zaidi ya kupokea raw data / training data
2. Activation function ina change value ya input, kwakua first layer inapokea training data, tunazitaka zibaki kwenye original form yake bila mabadiliko yoyote yale ili network iweze kujifunza kupitia hizo data

Kwahio, hakuna mahesabu yoyote ya kufanya kwenye first layer, hivyo output ya first layer ni original inputs kutoka kwenye training / raw data

Tutazame sasa outputs kwenye second layer

Ili iwe rahisi ku visualize, tuanze kukokotoa output ya node ya kwanza ya second layer

node ya kwanza ya tabaka la pili (second layer) inapokea input mbili, 1.0 na 0.5

Resultant sum (combined signal) ni jumla ya hizi inputs mbili:

Lakini, tunataka tu train neural network kwa ku adjust values za weights, so ili tu introduce weight kwenye mahesabu yetu, tunaweza sema kuwa, badala ya Combined signal (X) kuwa just sum ya incoming inputs, tunaweza zidisha kila incoming input na associated weight yake

Logic ya hapa ni simple ila ina nguvu, tunataka weight (strength of connection) baina ya node iwe na influence kwenye output ya hio node thus why tunazidisha weight baina ya hizo node na incoming signal yake

Tusema baada ya training, network ikajifunza kua hakuna haja ya hizo neuron kuzungumza (means w ikawa 0) basi hakutakua na output yoyote baina ya hizo neurons au nodes

So, combined signal kwenye node ya kwanza ya tabaka la pili ni:

Hivyo combined signal kwenye node ya kwanza ya second layer ni 1.05, lakini kumbuka tabia ya neuron ni ku suppress hii signal mpaka pale itakapokua strong enough
Tumeona pia hii tabia tunaweza kui model mathematically kwa ku apply activation function, kwa case yetu tumechagua Sigmoid function

Hivyo, output ya node ya kwanza kwenye second layer baada ya ku apply activation function itakua

Kama huna scientific calculator njia rahisi ya ku solve sigmoid function ni kuingiza tu value ya x kwenye form iliyo kwenye hii link (Note, output imekadiriwa to 4 decimal places)

Sigmoid Function Calculator

So output kutoka node ya kwanza ya second layer ni 0.7408

Tunaweza rudia mchakato huo huo kupata output ya node ya pili ya second layer

So, output kutoka node ya pili ya second layer ni 0.6457

Hivyo outputs ya hii simple neural network ni:

Utaona ni jinsi gani inachosha kukokotoa output ya hata neural network rahisi kama hii yenye node 4 tu
Vipi kama tuki deal na neural network yenye node hata 10, au 100. Inapaswa tuje na njia rahisi sana ya kufanya mehesabu yetu

Kabla sijamaliza, ngoja tu introduce baadhi ya terminologies zinazotumika sana kwenye neural network, tazama neural network yenye layers 3, kila layer ikiwa na nodes 3

First layer inajulikana kama input layer kwasababu ina represents input (raw data) kama zinavyoingia kwenye network, layer ya mwisho inajulikana kama output layer, kwasababu ndipo tunapopata output au prediction ya network nzima
Layer zote za katikati zinajulikana na hidden layer, sababu iliyofanya kupewa jina hili ni kwasababu output ya layers hizi huwa input ya layers nyingine zinazofata, kwa maneno mengine output inafichwa (hidden) kwa kugeuzwa kuwa input na hatuziona, tunachokipata ni output au prediction ya network nzima kwa ujumla

Tunaweza tumia mda huu ku formalize yote tuliyojifunza mpaka sasa

Why Activation Functions are Not Applied to the Input Layer​

In a neural network, activation functions are typically applied to the outputs of hidden layers and the output layer, but not to the input layer. Here are the reasons why activation functions are not applied to the input layer:

1. Input Layer Purpose:
   • The primary role of the input layer is to receive the input data and pass it into the network. Applying an activation function at this stage would modify the raw input data before it is processed by the network, which is generally not desirable.
2. Pre-processing Stage:
   • The input layer is essentially a pre-processing stage where the raw input data is introduced into the network without any modification. The data needs to be in its original form so that the first hidden layer can properly learn the initial features.
3. Linearity:
   • The first layer's job is to linearly transform the input data through multiplication by the weights and addition of biases. Applying an activation function at this stage would introduce non-linearity before the data has been properly weighted, which can disrupt the learning process.
4. Feature Learning:
   • The network needs to first learn to identify and weight the important features from the raw input data. Non-linear transformations are only beneficial after the initial feature extraction has taken place in the hidden layers.
5. Network Design:
   • Neural networks are designed to gradually build up complexity and abstraction as data moves from the input layer through the hidden layers to the output layer. Activation functions in hidden layers introduce non-linearities that allow the network to learn complex patterns. If the input layer were to apply an activation function, it would prematurely introduce complexity without adequate weighting and feature extraction.

Why We Multiply Incoming Signals with Weights​

Multiplying incoming signals by weights serves several critical purposes:

1. Feature Importance:
   • Weights adjust the influence of each input feature. During training, weights are learned such that important features get higher weights, and less important features get lower weights.
   • This allows the network to prioritize relevant information and ignore noise.
2. Linear Transformation:
   • The weight multiplication represents a linear transformation of the input space. This transformation helps in projecting the input data into a space where it can be better separated or classified.

Explanation:

• In a neural network, weights are the values that determine the strength of connections between neurons. These connections represent the relationships between different features of your input data.
• When a signal (input) travels through a neuron, it gets multiplied by the weight associated with that connection. This multiplication is a key part of how the neural network learns and makes predictions.

2. Linear Transformation

• Think of a linear transformation as a mathematical function that changes the shape or orientation of your data without introducing non-linear relationships.
• In our context, the weight multiplication acts as a linear transformation of the input space. This means it stretches, shrinks, rotates, or translates the original data points, but it doesn't fundamentally change the overall structure.

3. Projecting into a Better Space

• The goal of this linear transformation is to project the input data into a spacewhere it becomes easier to classify or separate. Here's why:
  • Better Separation: Imagine you have data points clustered together in a way that makes them hard to distinguish. By applying weight multiplication, you might be able to "spread" them out, making the different classes more obvious.
  • Feature Extraction: Weight multiplication can also help extract relevant features from the data. Imagine your input data is a picture of a cat. The weight multiplication might emphasize the edges or the shape of the cat, making it easier for the network to recognize it.

Input Layer​

The input layer of a neural network is the first layer of neurons that receives the raw input data. Here are its main characteristics:

1. Function:
   • The input layer serves as the entry point for the data into the neural network. It passes the raw input data to the next layer without any transformation or activation.
2. Neurons:
   • Each neuron in the input layer corresponds to one feature of the input data. For instance, if the input data is a vector of nnn features, the input layer will have nnn neurons.
3. No Activation Function:
   • Typically, the input layer does not have an activation function because its purpose is to simply receive and pass on the input data.

Hidden Layer​

Hidden layers are the intermediate layers between the input layer and the output layer in a neural network. They are called "hidden" because their values are not directly observed from the input or output data. Key characteristics of hidden layers include:

• Function: Process the input data by applying linear transformations followed by non-linear activation functions. This enables the network to learn and model complex patterns and relationships in the data.
• Neurons: Each hidden layer consists of multiple neurons, where each neuron receives input from the previous layer, applies a weight and bias, and passes the result through an activation function.
• Why "Hidden": Hidden layers are termed "hidden" because their outputs (also called activations) are not directly visible in the input or output. Instead, they are internal to the network, and their values are only used in intermediate computations.

Output Layer​

The output layer is the final layer in a neural network, producing the output of the network. Key characteristics of the output layer include:

• Function: Provides the final result of the network's computations. This result can be used for tasks such as classification, regression, or other predictions, depending on the network's design and purpose.
• Neurons: The number of neurons in the output layer depends on the specific task. For example, in a binary classification task, the output layer might have a single neuron producing a probability. In a multi-class classification task, the output layer might have one neuron per class.

Summary​

1. Input Layer: Receives and passes raw input data to the next layer.
2. Hidden Layer: Processes data through linear transformations and non-linear activations, learning complex patterns. Called "hidden" because its activations are not directly observed in the input or output.
3. Output Layer: Produces the final result of the network, tailored to the specific task.

By having these layers work together, a neural network can learn to approximate complex functions and make accurate predictions based on the input data.

Deep Neural Network (DNN)​

A Deep Neural Network (DNN) is a type of neural network with multiple layers between the input and output layers. The "deep" in deep learning refers to the number of layers through which the data is transformed. A network with more than three layers (including input and output) can be considered a deep neural network. Here’s a simple breakdown of what makes a DNN:

Characteristics of a Deep Neural Network:​

1. Multiple Layers:
   • Input Layer: Receives the raw input data.
   • Hidden Layers: Multiple layers that process the input data. These layers can number in the dozens or even hundreds in very deep networks. Each hidden layer learns to detect different features of the data.
   • Output Layer: Produces the final output, such as a classification or prediction.

Next : Matrix Multiplication is Useful .. Honest!

 

[Kuchwizzy]

Part 07 - Matrix Multiplication is Useful .. Honest!​

Kabla sijaendelea mbele, kuna concept ya msingi zaidi ambayo naona ni vyema kama nikiigusia kwa mara nyingine
Lengo kuu la huu uzi ni kuelewa Neural Network kama ilivyo (from the first principle), na kama umeshagundua, ni kuwa Neural Network ni just mathematical logic / concept zinazo try ku estimate au ku approximate physical working of real / biological neural network
(Tuta discuss zaidi different interpretations za Neural network kadri tutakavyoweza ili ujenge strong intuition ya Neural Network)

The keyword hapa ni Mathematics
Msingi wa ku master Machine Learning na Artificial intelligence kwa ujumla, ni hesabu, inapaswa kuelewa mathematical concepts and intuitions za neural network kadri unavyoweza

Mathematical concept ambayo nataka kuigusuia hapa ni Geometrical description of Neural Network
Jinsi gani Neural Network inafanya kazi from Geometrical point of view

Turudi tena kwenye XOR logic function, tumeona kua inputs za XOR function are not linearly separable
Huwezi ku draw single line inayotenganisha inputs (points) zinazo evaluate tu true, na zile zinazo evaluate tu false kwasababu zimechanganyika (scattered)

Tunweza ku visualize Input space ya XOR function kama ifatavyo:

Tuna maana gani tunaposema input space? kwenye Hisabati, space ni abstract concept tunayoweza kuitumia ku model aina yoyote ile ya taarifa (data), hivyo sio lazima iwe Physical space yenye dimensions tatu

Mfano kama input zetu ni maneno (words), kila neno linaweza kuwa represented kama point kwenye space fulani ya kufikirika (abstract) ya words space, na hii space inaweza kuwa na dimensions hata nyingi kadri utakavyo (higher dimensional space) kulingana na features tunazotaka Neural network ijifunze kutoka kwenye inputs

Visualization ya abstract embedding space (words space) huku kila nukta ikiwakilisha neno moja:

Sasa tutazame nini kinafanywa haswa na Neural Network during training kutokea kwenye Geometrical perspective

First layer ya neural network ama input inachofanya ku project original input space bila ku change chochote kwenye training dataset, kwa XOR function, original input space inaweza kuwa visualized kama ifutavyo (o ni true na x ni false):

Kwenye second hidden layer ndipo tunapo apply first weight multiplications ambayo ni just linear transformation (kwasababu tunazidisha input with a number), kwenye hii step, hatu change nature ya points (inputs) kwenye input space bali tuna change their location kwa transform original space kupata new space

Then tunapo apply activation function on combined signals kupata outputs za hio hidden layer, tuna perform aina ya pili ya transformation, a non linear transformation kwenye new space tuliyopata after first transformation (linear transformation by weights multiplication) kupata new space

Tuna repeat hii process kwa kila layer ya hidden layer, mpaka mwisho wa training, na kama tume train neural network yetu vizuri, tunapata new space ambayo points kwenye input space zipo linearly separable

Kwa case ya XOR function, hio new space inaweza kuwa visualized kama hivi (mfano tu):

And by "transform" means tunaweza ku scale, ku rotate, ku translate, ku reflect hio space n.k

So from geometrical perspective, neural network inachofanya ni ku transform original input space yenye non linear separation of inputs kwenda kwenye new and better input space yenye linear separation of inputs
Tuliona hakuna tofauti kati ya classification na prediction, means kama tunaweza ku separate then tunaweza ku predict

Huu ni mfano wa new and better words space, unaweza ona kwenye hii space maneno yenye maana sawa yapo karibu karibu (mfano neno "apple" lipo karibu na neno mac, macintosh na microsoft, neno "traffic" lipo karibu na neno "accident" au "buses" )
NB: Embedding space ndiyo inayotumiwa na Generative models haswa Large language model kuelewa context ya neno kwa kuangalia maneno yaliyo karibu na hilo neno kwenye words space

Unaweza visualize hii concept ya embedding kama upo interested nayo hapa:

Embedding Projector

Key take away hapa ni kwamba, kila layer ya hidden layer ina transform input space katika namna nyingi nyingi ili kupata possible set of new input space ambayo inputs ni linear separable
(Kwa lugha nyingine, tunasema kupata "curve" that best fits (describes) the data, hii statement sio lazima uielewe kwa sasa ila itakua clear kwako kadri tunavyozidi ku build intuitions))

Na kuna mahusiano makubwa kati ya Vectors, Matrices, Geometry na Linear Algebra kama tutakavyoona hapo mbele

Tuendelee sasa....
Lecture iliyopita tuliona ni jinsi gani inavyochosha kukokotoa output ya neural network hata ile neural network rahisi zaidi ya layers 2, kila layer ikiwa na node 2

Lazima tuje na njia rahisi ya ku compute output ya hidden layer bila kujali idadi ya nodi zake
Urahisi huu utakua sio msaada kwetu tu bali hata wakati tunapo code neural network
(Kumbuka, kama instructions ni rahisi kueleweka, ni rahisi pia ku turn hizo instructions into code)

Turudi kwenye ile simple neural network yenye layers mbili

Tuliona kua, combined signal kwenye hidden layer (layer 2) ni sum ya product ya weights na incoming signals

Tuseme, combined signals ni X
kwa kila node:

Hizo pairs mbili za namba (1.05,0.6) ni combined input to hii hidden layer. Naomba nifafanue kitu hapa, nitaangalia pia wapi nimefanya hii mistake then nitarekebisha
Ila pay attention nilipo bold, 1.05 na 0.6 ni combined input signals zinazokuja kwenye hidden layer, na sio output signals kutoka kwenye hidden layer
Tunapo apply activation function, ndipo tunapopata output signals za hidden layer husika ambazo zilikua 0.7408 na 0.6457. Hii ni point ya msingi sana kuielewa kwasababu itatusaidia sana huko mbele

Tukumbushane kidogo kuhusu rules za kuzidisha matrix, nadhani hii paragraph hapa chini ina summarize kwa usahihi rules of matrix multiplication unazopaswa kuzijua kwenye haya mahesabu tunayooenda kuyafanya

Number of rows za first matrix zinapaswa kuwa sawa na number of columns za second matrix, na zao la hizi matrix itakua ni matrix itakayorithi number of rows za first matrix na number of columns za second matrix
Matrix zinazofata hio sheria tunasema ni compatible matrix

Na hii ni general formula ya kuzidisha two compatible matrix:

Turudi tena kwenye neural network yetu (yenye layers 2, kila layer ikiwa na nodes 2)

Kumbuka, Matrix ni just rectangular array of numbers, symbols au function, so tunaweza ku arrange weight kati ya input layer (layer 1) na hidden layer (layer 2) kama Matrix of weights, W (kumbuka Matrix zinakua denoted kwa herufi kubwa, zikiwa bolded)

Tuki plug values za kila weight hapo juu tunapata:

Vile vile tunaweza arrange inputs kama Matrix, I

Tuki plug in values za kila input tunapata:

so tukizidisha hizo matrix mbili:

then,

Tazama hii resultant matrix

Utagundua kua ni combined input signals kwenda kwenye hidden layer tulizo kokotoa wakati ule this time zikiwa tu kwenye matrix form, kwa maneno mengine resultant matrix, tuseme X ni matrix of combined signals coming into hidden layer

So tumeona kuwa,

X ni matrix of combined signals into hidden layer, W ni matrix of weights kati ya input layer na hidden layer na I ni matrix ya original inputs into hidden layer (kabla ya weight multiplication)

Kabla hatuja generalize hio formula kwa usahihi zaidi, naomba nielezee terms ambazo zinaweza kukuchanganya
I ina represent original zinazokuja kwenye hidden layer, kwenye hio neural network yetu rahisi, tuna layer mbili tu, so second layer unaweza sema ni both hidden layer and output layer
Lakini tunaweza kuwa na more complex neural network yenye 3 layers (input layer, hidden layer na output layer)


Tuliona kuwa neural network yenye layers kwanzia tatu na kuendelea inajulikana kama deep neural network

Kwenye deep neural network yoyote ile, tuna one input layer yenye idadi yoyote ile ya nodes kulingana na nature of training data / inputs, na one output layer yenye idadi yoyote ile ya nodes kulingana na nature of outputs (kama ni prediction of continuous values (eg. the next word in a sentence) au classification of discret values (eg spam or not spam) na hidden layer yenye layers kwanzia moja na kuendelea

Kwakua first hidden layer ni input layer ya hidden layer iliyombele yake (second layer) na hii layer pia ni input layer ya hidden layer iliyo mbele yake (third hidden layer and so on), ni sahihi zaidi tukisema kuwa I ni matrix ya original input signals kutoka kwenye layer ya nyuma ya hidden layer (ya sasa)

Jambo la muhimu lingine ku note hapa ni kwamba, original input signals ambayo tumei represent kwa Matrix I, ni tofauti na combined input signals ambazo tumezi denote kwa Matrix X

Kumbuka, weights (strength of connection) kati ya node ina influence incoming original signals I, hii influence ndio inayotupa combined signals X

Kwahio ipi ni output sasa ya hidden layer ambayo itakua original input ya layer ya hidden layer ya mbele yake?

Mwanzo unakumbuka tuli apply activation function kwenye kila value ya combined signals (1.05 na 0.6) kupata output ya (0.7048 na 0.657) ambazo ndio output sasa za hidden

Tunafanya hivi hivi hata zikiwa kwenye matrix form, tunachofanya ni ku apply activation function kwenye kila element ya Matrix X

Hivyo output ya hidden layer yoyote ya neural network bila kujali idadi ya layers na nodes kwenye matrix form ni:

Nime reach limit ya 30 attachments, hii lecture inaishia kwenye post inayofata...

Bonyeza hapa

 

[Kuchwizzy]

=> => =>
So kama X ni

Tuki apply activation function kwenye kila element ya hio matrix, tunapata matrix O ya output

Hivyo, Generally, output ya hidden layer yoyote ya deep neural network yenye idadi yoyote ile ya layers na nodes hupatikana kupitia hii equation

O na X zikiwa matrix, huku x

W na I zikiwa matrix

Mwisho tumeweza kupata equation yenye form rahisi sana kuiandika kama computer instructions (code) na inayofanya kazi bila kujali idadi ya layers na nodes za neural network husika
Kama nodes na layers zikiwa nyingi hizo matrix zitakua kubwa tu (zitakua na elements nyingi ndani yake) ila form ya equation itabaki hivyo hivyo

Tunaweza tumia mda huu ku summarize tulichojifunza:

Key Points:
● The many calculations needed to feed a signal forward through a neural network canbe expressed as matrix multiplication.
● Expressing it as matrix multiplication makes it much more concisefor us to write, nomatter the size of neural network.
● More importantly, some computer programming languages understand matrixcalculations, and recognise that the underlying calculations are very similar. Thisallows them to do these calculations more efficientlyand quickly.
Simple explanation from Gemini 1.5 Flash:

1. Matrix Magic: All the calculations happening in this network can be written down as a special kind of math called "matrix multiplication." It's like a shortcut for lots of calculations.
2. Short and Sweet: This matrix way of writing things is much easier to understand and write down, even if the network is huge!
3. Computer Power: Computers are actually really good at understanding these matrix calculations. They see the pattern and can do them super fast! This makes your network work much faster.

So, basically, using matrix multiplication makes it easier to write down and faster for computers to understand the complex workings of a neural network.
Neural Networks as Transformers:

Neural networks are like magical machines that can reshape your input space. They learn how to transform your messy data points into a new space where things are much easier to separate.

• Imagine: Your neural network takes your mixed-up map (input space) and warps it, folds it, and stretches it. It's like you're making a new map, and on this new map, your cities are neatly arranged into separate clusters.

Linear Separability:

In this transformed space, a simple line can now easily separate your categories. This is called linear separability. Think of it like drawing a straight line on your new map to separate the cities into groups.

How It Works (Simplified):

1. Start: You begin with a messy input space.
2. Training: Your neural network learns from your data. It adjusts its internal "gears" to figure out how to reshape the space.
3. Transformation: The network transforms the input space, making it easier to separate data points.
4. Linear Separation: In the new space, categories can be separated with simple lines.

Key Points:

• Neural networks are powerful because they can learn to transform data into a space where it becomes easier to classify or analyze.
• This transformation is what allows them to handle complex, non-linear relationships in data.

Think of it like this:

• Input Space: Your original data points are scattered on a flat surface (like a piece of paper).
• Curve Fitting: You're trying to find a curve that best goes through those scattered points. This curve is like the "transformation" that the neural network learns.
• New Space: This curve essentially "lifts" the points off the flat surface and places them in a new space. It's like you're folding the piece of paper, changing its shape, and the data points move along with it.

How it relates to linear separability:

• Non-linear Separability: In the original flat space, your points are mixed up in a way that no straight line can separate them. It's like trying to draw a straight line to separate two groups of dots scattered on a piece of paper.
• Curve Fitting as Transformation: The neural network's transformation, like finding a curve, changes the shape of the space. It creates a "fold" or "warp" where the data points are now arranged in a way that a straight line can separate them. It's like folding the paper so the dots are now on different levels, making it easy to draw a line between them.

Example:

Let's say you have data points representing people's heights and weights. In the original space, you might have tall thin people, short heavy people, and everything in between. It's hard to separate these groups with a straight line.

A neural network, through its transformation, can find a curved surface that better fits the data. This surface could "lift" the tall thin people to a different "level" than the short heavy people, making it easy to draw a line separating them.

Key Takeaway:

Finding a curve that better fits the data is essentially what the neural network does by transforming the input space. It's a way to create a new space where the data is more structured and easier to analyze.

Prediction:

• Think of it as: Making a guess about something based on your knowledge of the data.
• In terms of space: You have a new input space where the data points are neatly organized. You take a new data point (like a new person's height and weight), put it into this transformed space, and then look at where it falls relative to the lines that separate different categories (like tall thin vs. short heavy).
• Output: Based on where the new point falls, you "predict" which category it belongs to.

Classification:

• Think of it as: Putting something into a specific group or category based on its characteristics.
• In terms of space: You're essentially assigning a label (like "tall thin" or "short heavy") to your new data point based on where it falls in the transformed space.

Why they're the same:

• The underlying process is the same: Both prediction and classification rely on the transformed input space to determine the most likely category for a new data point.
• Different words, same goal: We use "prediction" when we're making a guess about something uncertain. We use "classification" when we're assigning a definitive label.

Example:

• Prediction: You see a new person, and based on their height and weight, you "predict" that they are probably "tall thin."
• Classification: Based on the same information, you might "classify" them as "tall thin" after measuring their height and weight.

Key Takeaway:

Prediction and classification both rely on the ability of a neural network to transform the input space, making it easier to determine the most likely category for new data. They are essentially the same process, just with slightly different focuses.

Next : A Three Layer Example with Matrix Multiplication

 

[Kuchwizzy]

Huu uzi ni unaumiza kichwa sana, thus why audience ni wachache, ili nijue sipo peke yangu, kama unaufatilia huu uzi tangu mwanzo tunaweza peana feedback ya wapi pamekuchanganya so far au just comment chochote

 

[Kuchwizzy]

Lecture zitakua updated kama kuna kipengele kimekosewa au hakijaelezewa vizuri, kama ulisoma lecture 07 mwanzo, rudia upya

 

[Kuchwizzy]

Lectures zote zinazofata zimejengwa juu ya concepts tulizo discuss kwenye lectures zilizopita kwanzia ya kwanza
Hizi concept zote tunazi combine pamoja kupata final algorithm, make sure unaelewa kila lecture

 

[Nicklaus]

Somo nzuri lenye madini ya kutosha. Endelea kushusha nondo, nakufutilia kwa umakini.

 

[Andazi]

Huu uzi ni unaumiza kichwa sana, thus why audience ni wachache, ili nijue sipo peke yangu, kama unaufatilia huu uzi tangu mwanzo tunaweza peana feedback ya wapi pamekuchanganya so far au just comment chochote

Yani kaka nasoma nachoka nakaa pembeni narudi nachoka hasa ilipofika chapter 3 kwenda mbele dadeki

 

[Nicklaus]

Endelea kushusha vitu

 

[Kuchwizzy]

Yani kaka nasoma nachoka nakaa pembeni narudi nachoka hasa ilipofika chapter 3 kwenda mbele dadeki

Take your time, kuna concept nyingi za ku digest, ila once ukishaona jinsi gani zina fit together kama puzzle, utakua na most valuable knowledge kwenye A.I

 

[Kuchwizzy]

Endelea kushusha vitu

Nilikua busy kidogo, leo nashusha Lectures mbili

 

[Kuchwizzy]

Part 08 - A Three Layer Example with Matrix Multiplication​

Kwenye lectures zilizopita, tumeona jinsi gani ya kukokotoa output ya neural network kwa urahisi kwa kutumia Matrices
Tulitazama zaidi neural network yenye layers 2

Sasa tutazame jinsi gani njia hio hio inaweza kutumika kwenye neural network yenye layers tatu, kila layer ikiwa na neurons tatu.

Kwenye hiko kielelezo hapo juu, tunaweza kuona kuwa, inputs zetu ni 0.9, 0.1 na 0.8
Hivyo Input Matrix, I ni:

Tunaona pia kuwa associated weights (weights baina ya nodes au neurons za input layer na nodes au neurons za hidden layer) ni w11, w12, w13, w21, w22, w23, w23, w31, w32, na w33

Tufafanue hizo symbols zina maana gani ili zisije zikatuchanganya kwenye mahesabu
w11 = ni weight (strength of connection) kati ya node au neuron ya kwanza ya input layer na node au neuron ya kwanza ya hidden layer
(Analogy: weight ni kama waya kati ya hizo neurons mbili kama unaelewa zaidi kwa mifano)
w12 = ni weight kati ya node ya kwanza ya input layer na node ya pili ya hidden layer

Kwahio mifano michache, unaweza jua hizo symbol nyingine zilizobaki zina maana gani, mfano
w32 = ni weight kati ya node ya tatu ya input layer na node ya pili ya hidden layer

Kwenye hiko kielelezo, tumezitumia symbol hizo hizo ku represent associated weights kati ya neurons za hidden layer na neurons za output layer

Mfano
value ya w11 pia ni associated weight kati ya node ya kwanza ya hidden layer na node ya kwanza ya output layer
value ya w21 pia ni associated weight kati ya node ya pili ya hidden layer na node ya kwanza ya output layer

Logic hii hii inatumika kwa symbols nyingine (Tumefanya hivi ku avoid repetition)

Tukipanga hizo weights kama Matrix (tumeona jinsi hii njia ilivyo effective kwenye lecture iliyopita)

Tuki plug hizi values (rejea kwenye kielelezo) tunapata

Hivyo basi, combined moderated input kwenda kwenye hidden layer, x tutazipata kwa ku apply hii equation (unaikumbuka):

Baada ya kukokotoa (tumia scientific calculator au online tool yoyote kama unayo, ila ni easy pia hata ukifanya kwa mkono) tunapata

Now, tuna apply activation function kwa kila element ya hii matrix, X kupata Matrix O_hidden inayo represent output signals za hidden layer

Kumbuka kuwa:

Ila kumbuka, equation ya sigmoid function ni:

x ikiwa ni value ya kila element kwenye matrix X
Hivyo

So, tukichora upya kielelezo chetu, tunaona kuwa:

Hii ingekua ni neural network yenye layers 2 kama mwanzo tungeishia hapa, lakini kwa kua ni 3 layers neural network inabidi tu kokotoe pia output signal ya output layer ambayo ki msingi ndio ina represent final prediction ya network nzima

Process ni ile ile, kwenye hii stage, input matrix I (input signals zinazotoka kwenye hidden layer kwenda kwenye output layer ambazo zilikua ndio output za hidden layer), ni:

Na associated weight matrices, W kati ya nodes za hidden layer na nodes za output layer (rejea kielelezo kilichopita) ni:

So, combined moderated signals kutoka kwenye hidden layer kwenda kwenye output layer X, kama kawaida tunaipata kupitia hii expression (narudia sana hizi equations kwa sababu ni muhimu sana kwenye neural network programming hapo baadae, so zikumbuke):

So, X ni:

Now, tuchore upya kielelezo chetu kuonyesha combined moderated signal (kama zilivyokua represented na matrix, X) kwenda kwenye output layer

So, tunajua kupata output ya output layer tuna apply activation function kwenye kila element ya matrix, X:

So,

So,

Mwisho, tumepata output za output layer, so tu hariri kielelezo chetu:

Hongera!, tumeweza kufata signals kwanzia zinapoingia kwenye input layer mpaka zinapotoka kwenye output layer na kutupa prediction, tumeona mahesabu yote yanayofanyika

Kwa ufupi ni mahesabu haya haya yanafanyika kwenye deep neural network yenye ukubwa wowote ule (kumbuka neural network yoyote ile yenye layers zaidi ya 2 inakua considered kama deep neural network)

Trick ni ku treat kila layer independently

Kila node kwenye neural network inafanya kazi kubwa mbili

1. Ku calculated combined moderated input signal through linear transformation of matrix multiplication
2. Ku apply non linear transformation through activation function kwenye combined moderated signals ili ku produce output signal ambayo itakua input signal kwenda kwenye node ya layer inayofata

Tutumie mda huu ku formalize vyote tulivyojifunza:

1. Modular Design:

• Independent Computation: Each layer performs its own set of operations (matrix multiplication, activation function application) on its input. This means we can focus on understanding and implementing the calculations for a single layer without needing to know the specifics of other layers.
• Reusability: This modularity also allows us to reuse layer designs. If a specific layer structure works well in one network, it can potentially be incorporated into other networks without major changes.

2. Deep Network Construction:

• Scalability: The ability to build and train deep networks with many layers is enabled by this independent layer approach. We can easily add new layers without needing to re-implement the entire network from scratch.
• Hierarchical Feature Learning: Deep networks are able to learn increasingly complex features by stacking layers. Each layer builds on the representations learned in previous layers, which is facilitated by this independent layer design.

Example:

Imagine a deep network with 5 layers. Each layer can be seen as a separate module:

• Layer 1: Takes the input data and applies a linear transformation (matrix multiplication) and then a non-linear activation function.
• Layer 2: Takes the output from Layer 1 as its input and applies its own linear transformation and activation function.
• And so on...

By treating each layer as a self-contained unit, we can:

• Code and debug each layer individually.
• Easily add or remove layers without breaking the whole network.

In summary: The independence of layers in neural networks simplifies the design, implementation, and training of deep networks. It allows us to break down complex computations into smaller, manageable units, enabling scalability and efficient learning.

Why we choose matrices multiplication and activation function in our neural network computation?

Efficiency and Compact Representation:

• Matrix Multiplication: This is a highly optimized operation that can be performed extremely efficiently on modern hardware (GPUs, specialized matrix libraries). It allows us to compactly represent the linear transformations within a neural network. A single matrix multiplication can capture the weights connecting many neurons, making the computation concise and efficient.
• Activation Functions: These non-linear functions are applied element-wise to the results of matrix multiplication, introducing non-linearity crucial for learning complex patterns. They are also often computationally inexpensive, allowing for fast calculations.

Next : Learning Weights From More Than One Node

 

[50thebe]

Wazee wazee|

Kwanza nianze kwa kukiri kuwa sina kawaida ya kumalizia nyuzi ninazozianzisha kama ambavyo lecturers wengine wa JF walivyo pia, sababu kubwa huwa ni mbili, kukosa interest au kutingwa na kazi na mda mwingine unakosa wale sophisticated audiences unaowatarajia kulingana na topic husika

Ila huu uzi utakua tofauti, nitajitahidi kuu-keep active hata kama utachukua mwaka mzima, wachangiaji wa "kula tunda kimasihara" mbona wanaweza?

Tuanze......

Moja kati ya kitu ninachotakamani kujua pale ninapojifunza teknolojia yoyote ile ni jinsi ya ku replicate hio teknolojia kwanzia mwanzo kabisa (from the scratch)
Nikinukuu maneno ya Richard Feynman, "Kile nisichoweza kukitengeneza, siwezi kukielewa"

Ukweli ni kwamba ni ngumu sana ku create most of the tech (softwares) from the scratch, sababu huwa ni mbili

1. Too complex
2. Pointless

Tazama software kama Operating system? vipi kama tukiamua ku code from the scratch inatuchukua mda gani kupata non trivial, functional operating system? Too complex

Pia ni pointless, why reinventing the wheel wakati unaweza build O.S on the top of Linux kernel? au ukachukua Linux distro yoyote for free?

Lakini kama unataka kuelewa Operating System, huna budi ya kutengeneza moja from the scratch, sio lazima iwe complex kama Windows au Linux, but iwe minimal enough kufanya kazi.

Inspiration kubwa ya kuanzisha huu uzi, ni ujio wa Generattive AI, na kama una pay attention utagundua kuwa soon softwares nyingi zitakua integrated na hizi Gen AIs

Nyuma ya Generative AI revolution, kuna Transformer Architecture hii ndio core tech nyuma ya ChatGPT, Gemini, Llama na almost Generative foundation models zote kwasasa
Ukiaangalia hii architecture utagundua ni layers za Neural networks tu zilizopangwa katika mtindo mzuri

Means, kama utaelewa Neural network vizuri, unatakua na uwezo wa kuelewa sio tu Transformer architecture ila A.I field kwa ujumla kwasababu ina rely zaidi kwenye Neural network kama dominant ML Algorithm

Na njia pekee ya kuelewa Neural Network? Yah unda yako from the scratch

Tofauti ya Neural network na Operating system ni kwamba Neural network sio ngumu kabisa kuiunda from the scratch
Na ninaposema from the scratch, sina maana ya codes tu, bali kwanzia theory, mathematical formalism, coding, training mpaka evaluation yake.

Mathematical concepts nyuma ya Neural network zote tumezisoma form 5 & 6 sio complex, kwa asilimia kubwa ni Differentiation, Matrix, Functions, na Vectors plus concept kadhaa kwenye Biology

So lengo la huu uzi ni ku design na ku code algorithm ya neural network from the scratch......(kwanzia theory, mathematics , programming mpaka training na evaluation)

Prerequisites: Na assume upo comfortable na Python Programming, na una fundamentals za Pure mathematics haswa topics kama Matrices, Logic, Function, na Calculus, na basic concepts za Linear Algebra
Una PC na Gmail account plus passion ya ku digest hizi concept zote

Link ya lectures hizi hapa chini (kwasasa tupo Lecture 7).

Lecture 1 - Easy For Me, Hard For You
Lecture 2 - A Simple Predicting Machine
Lecture 3 - Classifying is Not Very Different from Predicting
Lecture 4 - Sometimes One Classifier Is Not Enough
Lecture 5 - Neurons, Nature’s Computing Machines
Lecture 6 - Following Signals Through A Neural Network
Lecture 7 - Matrix Multiplication is Useful .. Honest!


+255748333586

GitHub link iko wapi mwamba!

 

[Kuchwizzy]

GitHub link iko wapi mwamba!

Link ya? (Bado hatujafika kwenye programming)

 

[Andazi]

Ngoja nikalale nahisi kupasuka sasa

 

[Kuchwizzy]

Part 09 - Learning Weights From More Than One Node​

Wakati tunajiunza kuhusu linear classifier, tuliona kua, linear classifier inajifunza kwa kurekebisha (adjust) parameter yake (slope or gradient of the straight line) kulingana na error (E) iliyopatikana wakati inajaribu ku predict value ya training input data, X kwa kiasi fulani, dA

Tuliona jinsi gani ilivyokua rahisi kupata hii Expression:

L ikiwa ni Learning rate

Sasa tujaribu kutafuta equivalent expression kwenye neural network itakayotusaidia kujua kwa kiasi gani tunapaswa ku adjust value ya parameter yetu, ambayo kwenye neural network ni weight (W), kulingana na error (E) tuliyopata wakati tuna predict output ya training input data (X)

Tushajua jinsi ya kukokotoa X (moderated input signal), na Output, O ya neural network
Vilevile tunajua kuwa, Error (E) ni tofauti ya Output (au prediction), O ya network na target au actual value

(Rejea hizo expressions kwenye lectures zilizopita, najaribu kutumia maximum number of attachments allowed per post vizuri)
So kwenye neural network, tunajuaje ni kiasi gani tunapaswa ku adjust value of weight?

Ukifikiria kwa haraka haraka tu, utaona kuna tofauti moja, kwenye simple linear classifier tulikua tuna deal na parameter moja tu, lakini kwenye neural network, tuna multiple weights associated baina ya nodes, so tuna parameters zaidi ya moja

Vilevile, kumbuka tunapaswa kutumia value ya error, E ku update kila weight, lakini output ya network nzima imekua affected na kila weights, hivyo haiingi akilini kutumia value yote ye error ku update single weight

Kama hayo maelezo juu yanakuchanganya, imagine huu mfano

Scenario 1:
Tuna mtu mmoja anayepandisha bendera, tunataka bendera iwe umbali fulani kwenye mlingoti (target value)
Huyu mtu akikosea (error), kumrekebisha ni rahisi kwasababu yupo peke yake, tunaweza kumwambia ashushe kidogo au apandishe (adjusting the slope)

Scenario 2:
Tuna kundi la watu linalopandisha container la matofari kwenda ghorofa ya pili (target value), hawa watu wakikosea
ni ngumu kuwerekebisha kwa kumwambia mtu mmoja mmoja, kwasababu kila mtu anachangia kwenye nguvu moja inayotumika kunyanyua hilo container (multiple weights), na kila mtu anauwezo tofauti, kuna wapo waliosukuma zaidi kuliko wengine (different weight value), so ku adjust position ya container (output) tunapaswa kujua kwanza kabla ya yote, kwa kiasi gani kila mtu (weight) amechangia kwenye makosa yaliyofanyika (error)

Kila mtu anapaswa kujua makosa yake (weight's contribution to overall error), sasa ni makosa kiasi gani kila mtu (weight) amechangia kwenye makosa ya jumla (Error)

Solution rahisi ni kujua sehemu ya kosa ambalo kila weight ime contribute

Tazama hiki kielelezo:

Kama overall error iliyopatikana ni E, tunapaswa kujua ni kwa kiasi gani w11 imechangia kwenye hio error, tuiite e11
na kwa kiasi gani w21, imechangia kwenye hio error, tuiite e21

Solution rahisi ni kuzidisha overall error E, na kiasi cha influence (weight) ambacho kila weight ime contribute kwenye overall weight iliyo influence ouput, ambayo imeleta hio error

Concept rahisi ya ratio theorem inaweza kutusaidia

Unaweza kuona jinsi gani hii equation ina make sense, lengo letu ni kila weight ipate its share of error ambayo itatumika kwenye expression (ambayo bado hatujaipata) ya ku adjust value yake

Kama kila weight ina equal contribution, kwa maneno mengine, w11 = w21, then kila weight itapata nusu ya overall error

Kwa maneno mengine, tunagawanya error ili ku assign error kubwa kwenda kwenye weight kubwa, na error ndogo kwenda kwenye weight ndogo, logic ambayo ina make sense kwasababu weight kubwa imechangia zaidi kwenye overall error kuliko weight ndogo

Kama umeshagundua, tunatumia weights katika namna mbili

1. Kusafirisha (propagate) signals into the network up to output layer
2.Kusafirisha (propagate) errors back into the network ili network ijifunze kulingana na makosa yake
Ndio maana hii njia inaitwa Backpropagation (shika hii term, ni moja kati ya terms muhimu kwenye A.I na Machine learning kwa ujumla)

# Backpropagating Errors From More Output Nodes

Neural network tuliyotoka kuitazama, ni very simple, ina layer 2 na output node moja
Vipi kwa neural network complex kidogo, yenye output layer yenye nodes zaidi ya moja?

Hapa pia hakuna tatizo, kuwa na output zaidi ya moja haituzuii kutumia njia ile ile tuliyotumia hapo mwanzo wakati tuna deal na layer yenye output node moja, sababu kwanini tunaweza kufanya hivi ni kwamba calculation ya kila node ni independent na calculation ya node nyingine, kwasababu kila node ina associated weights pair zake ambazo ni independent za nodes nyingine

Utaona kwenye hiko kielelezo, weights baina ya input layer na node ya kwanza ya output layer ni w11 na moja w21
Na weights baina ya input layer na node ya pili ya output layer ni w12 na w22

Haziingiliani, hivyo error propagation kati ya hizo nodes mbili zinawezwa fanya independently

# Backpropagating Errors To More Layers

Sasa tutazame network complex zaidi ya hizo, yenye layers zaidi ya mbili (yaani deep neural network)

ni weights kati ya nodes za output layer na nodes za hidden layer
eoutput

Ni errors za output layer tulizopata kwa ku split overall errors with proportional to each weights kama tulivyoona hapo awali, tumetumia label ya pamoja kama tulivyofanya kwa weights

Hio ilikua ni baina ya hidden layer na output layer

Kati ya hidden layer na input layer, process ni ile ile haibadiliki, tuta calculate errors (tuna split overall errors with proportional to each weights) baina ya hidden layer na input layer

ni errors kati ya hidden layer na input layer, tumezi label kwa pamoja

ni weights kati ya input layer na hidden layer, tumezi label kwa pamoja

Na hata kama tungekua na layers nyingine zaidi, tunge repeat tu mchakato huu huu

Sasa kipengele kinakuja hapa, errors kati ya hidden layer na output layer tuliipata kwa ku split overall error
according to each weights
Lakini overall errors tunajua ni tofauti kati ya output ya final layer / output layer na target value kutoka kwenye training data

Tukitumia mantiki hio hio kati ya input layer na hidden layer, overall errors inatakiwa kuwa tofauti ya output na target value
Tayari tunajua jinsi ya ku calculate output ya layer yoyote ile, lakini ipi ni target value kati ya input layer na hidden layer
Au target value baina ya hidden layer?

Jibu ni kwamba, hatujui ipi inapaswa kuwa target value ya hidden layer, training data zinatwambia tu ipi inapaswa kuwa target value ya output layer (final layer) lakini haitwambii ipi inapaswa kuwa target values za hidden layers

Hivyo kwa case hii, mbinu yetu ya kukokotoa error kama tofauti ya output na target value, haiwezi kufanya kazi

Tunapaswa kuja na mbinu nyingine ya kukokotoa errors baina ya hidden layer.

Bofya hapa kuendelea

 

[Andazi]

Ulitumia muda gani kujifunza hivi vitu

 

[Kuchwizzy]

Part 09 - Learning Weights From More Than One Node (Inaendelea...)​

Twende taratibu kwenye hii concept tusije tukachanganyana, kwasababu ni muhimu sana kuelewa tunamaanisha nini hapa

Tutazame hiki kielelezo hapa chini:

t1 = ni target value kwenye node ya kwanza ya output layer
t2 = ni target value kwenye node ya pili ya output layer
e1 = ni error kwenye node ya kwanza ya input layer / hidden layer / output layer (nimetumia symbol moja ku denotes hizo errors zote, haina maana kuwa lazima ziwe sawa)
w11, w12, 21, na w22 hizi hazina haja ya introduction, tayari tunajua zinawakilisha nini

Kiini cha tatizo hapa ni kwamba, tunajua output ya nodes zote za output layer zinapaswa kuwa vipi kwasababu training data zinatwambia lipi ni linapaswa kuwa jibu sahihi (target value) kwa kila node ya output layer

Hivyo e1 na e2 za output layer tunaweza zipata kwa kukokotoa tofauti kati ya output na prediction kama kawaida

Lakini hatuwezi ku kokotoa e1 na e2 za hidden na input layer kwasababu hatujui target values ya nodes za hizo layers zinapaswa kuwa vipi
Training dataset zinatupa target values ya nodes za output layer tu

Sasa tunapata vipi values za e1 na e2 za hidden na input layers kama hatujui target values inayopaswa kufikiwa na nodes ya hizo layers?

Kupata jawabu, tu focus kwanza kwenye output layer, kwasababu tunajua jinsi ya kupata values za e1 na e2

Tunajua kuwa, kupitia back propagation of errors, error za e1 na e2 zitagawanywa kwenda kwenye kila weights iliyo contribute kwenye hizo errors kulingana na weights zao

Tutazame huu mgawanyo wa errors kati ya nodes za output layer na node ya kwanza ya hidden layer

Awali tuliona kuwa, wakati tuna split (propagate) errors, kuna fraction ya e1 ambayo itatumika ku update weight w11, tuiite e11 (kwasababu itatumika ku adjust weight kati ya node ya kwanza ya output layer na node ya kwanza ya hidden layer)

Vilevile, fraction ya e2 itatumika ku refine (adjust) weight w12, tuiite e21

Mathematically, tunasema kuwa:

Kuna point ya msingi hapa ya kuitambua, kuna sehemu za e1 na e2 zitatumika ku adjust weights kati ya node ya kwanza ya hidden layer na nodes za output layer zilizoungana nayo
Kwasababu huo muungano umeifanya node ya kwanza ya hidden layer ku influence sehemu ya output ya hizo nodes za input layer zilizoungana nayo, hivyo its share of error inapaswa kuwa propagated backward kuja tena kwenye hio node kwa ajili ya ku adjust hizo weight

Key take away ni kwamba kila node kwenye hidden layer ina effect output ya nodes za mbele yake zilizoungana nayo

"The error at an output node is split and distributed back to the hidden nodes that contributed to it"

Sasa tuseme error ya node ya kwanza ya hidden error ni

Kwasababu hatuwezi tumia njia tuliyoitumia kupata errors za nodes za output layer, tunaweza sema kuwa error katika hii node ni jumla ya fractions of errors ambazo zinakua propagated back to this node

ambazo ni e11 na e22, so:

Kimsingi tunaweza generalize hii mbinu ku calculate error ya node yoyote ile ya hidden layer bila kujali number of layers, simply tu kwa kutafuta sum of split errors propagated back to it

Tuki expand hio expression, tutaona

"The error for a hidden node is the sum of the split errors from all the output nodes it connects to"

Tuione hii theory in action:

Tu calculate errors zote ambazo zitapaswa kuwa propagated back into the network kwanzia kwenye output layer kama tulivyofanya wakati wa ku propagate signals from input to output layer

Lengo ni kujua calculations zote zinazokua involved (unaweza ku zoom hiki kielelezo kama huoni hizo values vizuri)

Tuone hizi calculations zimefanyikaje
Kupata error ya node ya kwanza ya hidden layer, e1 tunachukua sum of split errors from all output nodes zilizoungana nayo
Tukitazama hiko kielelezo, tunaona kuwa associated weights baina ya hii node na output nodes zinazoungana nayo ni
2.0, na 3.0, pamoja na 1.0 na 4.0 (tazama huo mchoro kwa makini)
Huku overall errors zikiwa ni e1 = 1.5 na e2 = 0.5

So split (fractions of) errors za e1 na e2 ambazo zitakua propagated back to hii node ni

Note w11 = 2.0, w21 = 3.0

Na

Adding up those errors tunapata:

Ambayo ndo itakua error ya node ya kwanza ya hidden layer, e2

Tunatumia njia hii kupata error ya node ya pili ya hidden layer

na

Adding up those errors tunapata:

Process hii hii tunaitumia ku calculate errors na input nodes, (unaweza ku try out wewe mwenyewe, sitorudia tena calculations kwasababu ni zile zile)

Hongera!, sasa tumeona jinsi gani ya ku propagate errors back into the network, tumeona calculations zote zinazofanyika kama tulivyoona wakati tuna propagate signal into the network

Tunapo propagate signals / inputs into the network from input to output layer, hii process inaitwa forward pass
Tunapo propagate errors back into the network from output to input layer hii process inaitwa backpropagation

Tunaweza kutumia mda huu sasa ku formalize yote tuliyojifunza:

Forward Pass:​

The forward pass is the process where the input data is passed through the neural network to produce an output. Here's how it works:

• Input: The network takes in input data (e.g., images, text, etc.).
• Layer-wise Computation: The data is passed through each layer of the network. Each layer applies its transformation, typically consisting of a linear transformation (using weights) followed by a non-linear activation function.
• Output: The final layer produces the output of the network, such as class scores in a classification task.

The forward pass is essentially the prediction phase, where the network processes the input data to generate an output based on the current state of its weights.

Backpropagation is the central algorithm for training artificial neural networks. It's the process of adjusting the network's weights to minimize the error between its predictions (from the forward pass) and the actual target values in the training data.

Here's how it works:

1. Forward Pass: As we discussed, the forward pass calculates the network's output for a given input.
2. Error Calculation: The difference between the network's output and the target output from the training data is calculated. This difference is called the error or loss.
3. Backwards Propagation of Error: The error is then propagated back through the network, from the output layer to the input layer. At each layer:

Splitting and Recombining Errors:

• Splitting: The error at an output node is split and distributed back to the hidden nodes that contributed to it. The amount of error assigned to each hidden node is proportional to the strength of the connection (weight) between the hidden node and the output node.
• Recombining: The error for a hidden node is the sum of the split errors from all the output nodes it connects to.

Neural networks learn by adjusting the weights of their connections, a process guided by the error, which is the difference between the correct output (provided by the training data) and the network's actual output.

• The error at the output nodes is straightforward to calculate as the difference between the expected output and the actual output.
• However, determining the error for internal nodes is more complex. A common approach involves distributing the errors from the output layer back through the network, proportionally to the weights of the connections. These distributed errors are then aggregated at each internal node.

Next : Backpropagating Errors with Matrix Multiplication

 

[Kuchwizzy]

​

Ulitumia muda gani kujifunza hivi vitu

Upo lecture ya ngapi?