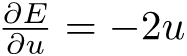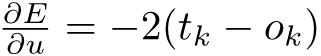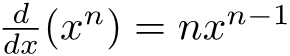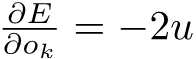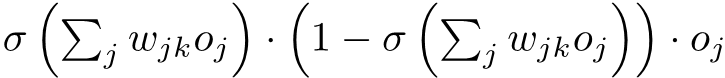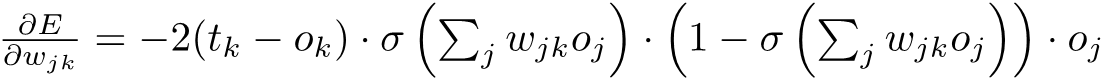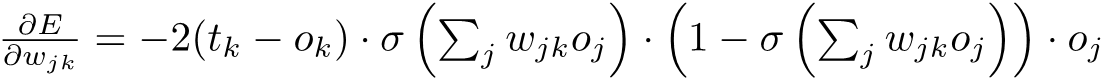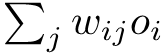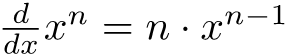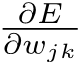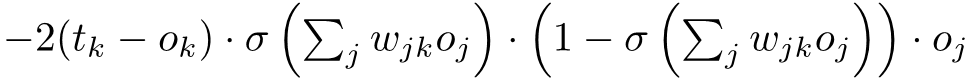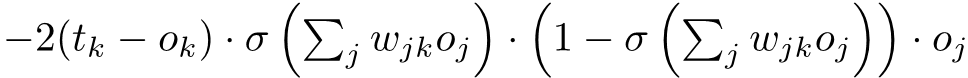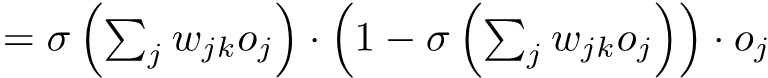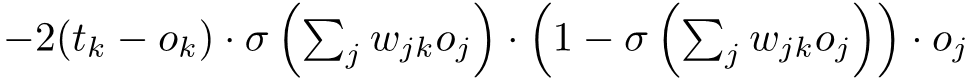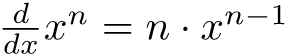Create Your Own Neural Network From The Scratch (A.I - 101)

[Kuchwizzy]

Part 13 - Mean Squared Error ( Loss ) Function And Mathematics of Gradient Descent Algorithm​

Tangu mwanzo, tuliona kuwa Error, ni tofauti kati ya network prediction, O na target value from the training dataset, T

Ni equation rahisi sana, inapima tofauti kati ya output na target value na kazi yetu ni kupunguza hio tofauti kadri tunavyoweza, lakini je inatufaa tunapoelekea?

NB: Error function ina majina mengi, kuna Error function, Loss function na Cost function. Pote tunazungumzia kitu kimoja, kuna cases nyingine, tofauti inaweza kuwepo, ila mda mwingi hizo terms ni interchangeably

Hii table hapa chini inaonyesha Error functions za aina tatu ikiwemo hii

Tuna network output, O, tuna target output T, na aina tatu za error functions

Ya kwanza, ni simple difference kati ya output na target tunayoijua, udhaifu wa hii approach ni kwamba kama tukitaka kujua overall performance ya network nzima kwa kujumlisha errors zote
Hii error function ina tabia ya ku cancel baadhi ya errors na kutupa wrong judgement ya network performance

Utaona kwenye hio table, tukichukua jumla ya errors zote tunapata 0, ikiwa na maana kuwa overall network haina errors (ina perform better) licha ya kuwa imetupa incorrect prediction mbili (0.5 badala ya 0.4, na 0.7 badala ya 0.8)

The reason ni kwamba, negative na positive errors zina cancel each other, hata kama hazitoji cancel completely na kuwa 0, utaona kuwa sio njia nzuri ya kupima network error

Aina ya pili ya error function ni kutake absolute values of errors (inachukua only positive values) ku avoid cancellation of errors
Ubaya wa hii approach ni kwamba, Absolute function hazina smooth curve, ni discontinuous pale inapo approach minimum values (eg at

), hivyo sio differentiable

Hii ni graph ya simple absolute function kuona tunachomaanisha:

Tuliona kuwa ili function iwe differentiable, inapaswa ku change smoothly as its parameters changes bila kuwepo kwa discontinuities au abrupt change (mabadiliko ya ghafla) ya aina yoyote, ila utaona kuwa x inapo approach 0 (at x = 0), absolute function ina jump ghafla (from decreasing to increasing or viceversa)
Hatuwezi kutumia hii approach kwasababu algorithm ya gradient descent ambayo inategemea differentiability ya function kufanya kazi (its first derivative) haitoweza ku deal na V shaped curve ya aina hii. Vilevile slope yake haipungui as we approach its local minimum, so kuna risk ya ku overshoot na ku bounce hapo hapo milele.

Aina ya tatu ya Error function, ni square error function, means tuna square tu Error function yetu tuliyoizoea

Tayari tunajua kuwa squared error function ni differentiable, zina changes smoothly as its variables change at any point on the graph, so tume solve tatizo letu la errors kuji cancel na bado tuna advantage ya kutumia Gradient descent

Hii candidate ya error function ina advantage nyingine pia, ni rahisi kutafuta derivative ya squared function, so inakua rahisi hata kwenye computation.

Mathematics of the Gradient Descent

Kama tuna imagine overall Error function kama curve, basi kila weight kwenye neural network ita represent a particular location au point kwenye hio curve

Hii ni 2D (plane) representation ya tulichosema hapo juu

Sasa tunachopaswa kujua, ni slope au gradient ya Error function katika hio location au weight (generally, any location au weight), kwenye huo mchoro hapo juu

ina represent any particular weight kwenye neural network na

ni slope ya error function with respect to this weight ONLY, formally hii ni partial derivative ya Error with respect to this weight huku tuki assume other weights as constant

(Kihesabu hakuna tofauti kati normal derivative uliyozoe na partial derivate, tofauti ni kwamba in partial derivative tuna differentiate the function with respect to only one variable, while keeping other constant. kwenye hii case yetu tunataka kujua gradient of the error function katika hii particular variable, so hatuna haja ya kujali kuhusu all other weights, we keep them constant
Tunatumia partial derivative tunapo deal na multivariate function kama kwenye hii case)

Hapa tunashauku ya kujua direction of the slope ili tu move hii weight in opposite direction

Sasa tutazame hii diagram hapa, ni simple neural network yenye 3 layers, kila layer ikiwa na 2 neurons

Japokua tuta reference hii diagram, tuta generalize derivation yetu ku fit any neural network of any size.

Tutazame notation kwenye hio diagram:

ina represent any input signal into the network

ina represent any weight connecting any node from the input layer to any node in the hidden layer

ina represent any weight connecting any node from the hidden layer to any node in output layer, in case of hidden layer, hii ita represent any weight connecting any node from the previous layer to any node in the current (or next) layer. Kumbuka output ya one hidden layer ina save kama input ya next hidden layer

ina represent final output ya neural network at any output node

ni jumla ya backpropagated error from the hidden layer (jumla ya errors zote za hidden layer zinazokua propagated back to input layer)

ni target value at any output node (hii value ni constant kwasababu inatoka kwenye training data)

zina represent any particular node in the input layer (i), hidden layer (j) na output layer (k)

Kama unavyoona, tumehakikisha tunakua as general as possible ili final equation yetu ifit any neural network of any size

Kwa kuanza, tu focus na weight kati ya node yoyote ya hidden layer iliyounganisha node yoyote ya output layer
Kwenye notation zetu hapo juu, hii particular weight tumeiita

So, imagine tupo juu ya huu mlima wa Error function (kwenye deep neural network, hii very complex higher dimensional space),

katika hii location

na tunataka kujua ni wapi pana muinuko (slope or gradient) ili tuendee ulekeo tofauti na huo muinuko (kumbuka hatuna ramani, hatujui wapi kuna mteremko, so best option ni kucheki wapi kuna muinuko ili tusielekee huko, hii ndio logic nzima ya Gradient descent)
Na kumbuka kuwa, tuna focus only on this weight, tuna ignore nyingine zote

Hivyo kihesabu, tunapaswa tu compute partial derivate ya Error

with respect to this weight

ambayo ndio muinuko (gradient) wa huu mlima (space of error) kwenye hii location (weight)

Mathematically, hio gradient ni

But

ni summation ya all squared errors in output nodes (Kumbuka tunatumia squared error function sasa kama our best error function kwasababu tulizoziona kwenye lecture iliyopita)

So,

ni instance au index ya particular output node (it can range from n = 1 to n = n, basically any number depend on size ya neural network uliyo design)

ni target value katika hio particular node

ni output or prediction ilyofanywa na hio node

So, tuki expand our expression tunapata hiki:

Sasa, tu expand our sigma notation

Kama tunavyoona, tunapaswa ku take derivative ya kila instance ya squared error with respect to weight

Hii ni gharama kihesabu (computationally expensive) ukizingatia tunaweza kuwa na maelfu hata mabilion ya hizi instances kulingana na idadi ya output neurons / nodes

Lakini tukumbuke kuhusu tulichojifunza wakati wa forward pass, kila weight ina influence output ya neuron ambayo imeunganishwa nayo na haina influence kwenye output ya node ambayo haijaunganishwa nayo
Ndio maana tunapo propagate errors back wakati wa backpropagation kila node ina share its fraction of errors kutoka kwenye output nodes zilizoungana nayo

Inaendelea....

 

[Kuchwizzy]

ni single particular weight, assume inaunganisha any node

from hidden layer, with any node

in the ouput layer
so ina influence kwenye output node ya hio node pekee na sio kwenye node nyingine

Kwa maneno mengine

ina influence tu kwenye output

ambapo

Hivyo derivative ya squared errors nyingine with respect to

ni

isipokua kwenye squared error ambapo

So, kwahio logic tumeweza ku simplify kwa kiwango kikubwa sana our calculation

Tukiondoa hizo 0 tunapata hii simpler expression

Licha ya simplification tuliyofanya, still tunapaswa kutafuta derivative ya

with respect to

Lakini tunajua kuwa

nayo ni function ya

kwasababu value yake imekua influenced na

wakati wa linear transformation through weights multiplication (note, incoming signal tunai treat kama constant kwenye hii stage, so only real variable ya

ni weight

)

Kwa kusema hivi, ni wazi hapa tuna deal na composite function kwasababu tuna try kufafuta derivative ya function (error) with respect to variable (weight) which is also a variable of another function (output) in the same expression

Ladies & gentlemen......

The Chain Rule​

Utaikumbuka hii rule kwenye pure paper 1.

If a variable z depends on the variable y, which itself depends on the variable x (that is, y and z are dependent variables), then z depends on x as well, via the intermediate variable y. In this case, the chain rule is expressed as

kwenye case yetu,

ni

,

ni

na

ni

ili kupata derivative ya error with respect to weight

ni lazima tutafute kwanza derivative ya error with
respect to output

pamoja na derivative ya output with respect to weight

kwa mujibu wa Chain rule.

Tuanze na derivative ya Error with respect to output

Inaendelea.....

 

[Kuchwizzy]

(Kuna limit ya 30 max attachments, kwa hii derivation, itatuchukua multiple posts)

Tuanze na derivative ya Error with respect to output,

Tusema,

, hivyo

(kumbuka ni equation tu ya squared error iliyobaki)

Hivyo

Now, tu apply power rule ku compute derivative of error with respect to u (function of output)

Power rule​

The power rule is used to find the slope of polynomial functions and any other function that contains an exponent with a real number. In other words, it helps to take the derivative of a variable raised to a power (exponent).

Tunapata

Then, imebaki derivative of ya u with respect to output,

Hii ni rahisi, kumbuka

huku

ikiwa ni constant (it is target value from the training data katika hii node), so derivative ni simply

Tuki tafuta sasa product ya hizo derivatives according to the chain rule, tunapata

Kumbuka

, so

Hivyo basi,

ni

Lakini tukumbuke kuwa

tunaipata kwa ku apply sigmoid function kwenye combined moderated signals from hidden layer, so mathematically

ikiwa ni input kutoka kwenye node ya hidden layer

Now, tuki expand our equation

Sasa tu focus kwenye hii part ya equation

Tu assign label kwenye hii composite function kama tulivyofanya hapo juu

(Utaona kuwa tunataka kutafuta derivative ya hii function nzima with respect to weight,

, lakini weight pia ni variable kwenye sigmoid function)
Inaendelea....

 

[Kuchwizzy]

Then tu apply chain rule kama mwanzo:

Tuanze na first part, ambayo kimsingi ni derivative ya sigmoid function,

Hapa hatuna haja ya kupiga hesabu, tunatumia standard result ya derivative ya sigmoid function ambayo ni:

Imeisha hio, tuhamie kwenye hio derivative ya pili, derivative of u with respect to weight,

Kumbuka

, so

But tuki expand hio sigma notation:

Tunapata

Kama mwanzo, tunapaswa ku compute derivative ya each term, lakini utaona kuwa expression nyingine zote ambazo hazi contain

kimsingi hazi change with respect to it, kwasababu outputs

haziwi influenced na weight

, na

tume zi keep constant (kumbuka hii operation nzima ni partial derivative) so derivative katika hizo terms simply ni

Kwa part ambayo ime contain our weight, derivative ya

with respect to itself ni

so tunabaki na our constant term ambayo ni

so

But

so

Finally, derivative of Error

of the neural network, with respect to any weight between hidden and output layer

,

Ni

Kwa kivumbi na jasho, tume derive expression ambayo inatumika ku compute gradient of the error function with respect to any weight between hidden and input layer

Hii ni full expression:

.

 

[Kuchwizzy]

Tutumie huu mda ku formalize tulichojifunza mpaka sasa:

1. Partial Derivative​

In the context of neural networks, a partial derivative represents the rate of change of a function (typically a loss function) with respect to one of its input variables, while keeping the other variables constant. Specifically, when training a neural network, we compute the partial derivatives of the loss function with respect to each weight in the network to understand how small changes in that weight will affect the overall loss.

2. Chain Rule​

The chain rule is a fundamental rule in calculus used to compute the derivative of a composite function. In neural networks, the chain rule is used extensively during backpropagation, a process where we calculate the gradients of the loss function with respect to each weight.

3. Power Rule​

The power rule is a basic derivative rule in calculus, which states that:

4. Why Weight Only Influences the Output of the Node It Is Associated With​

In a neural network, each weight is associated with a specific connection between two neurons. Therefore, the effect of a weight change is localized to the node (neuron) it is directly connected to, which in turn influences the output of that specific node.

5. Why This Fact Simplifies Gradient Descent Calculation​

The fact that a weight only influences the output of the node it is associated with simplifies the gradient descent calculation because it allows us to break down the problem into smaller, more manageable pieces. When computing the gradient of the loss with respect to a particular weight, we only need to consider how changes in that weight affect the specific node's output, rather than having to account for the entire network all at once.
During backpropagation, we can calculate the gradient of the loss with respect to each weight individually, then update each weight accordingly. This locality reduces the computational complexity and makes it feasible to train large neural networks efficiently using gradient descent and its variants (like stochastic gradient descent)

Next: Derivative of Error with respect to any weight between input and hidden layers.

 

[singanojr]

Data science na Machine learning bila kuiva kwenye hesabu hutoboi

 

[Kuchwizzy]

Part 14 - Derivative of Error with respect to any weight between input and hidden layers.​

Kwenye lecture iliyopita, tuliona jinsi gani ya ku compute the gradient of the error function

with respect to any weight kati ya any node of the hidden layer na any node of the output layer

Sasa tunapaswa ku compute derivative of the error function

with respect to any weight kati ya any node of the input layer na any node of the hiddenlayer

Mathematically, tunapaswa ku compute

Badala ya ku derive upya, tunaweza kutumia symmetry na physical interpretation ya equation ya

Tutazame kila sehemu ya hio equation na physical interpretation yake:

hii interpretation yake ni simple, ni just error, difference kati ya target value na predicted value katika any instance of the output node
Kwasababu training data hazitwambi ipi ni target value inayopaswa kufikiwa na node za hidden layer, tunaweza equate hii expression with back propagated error kutoka kwenye hidden nodes

ina represents sum of the combined moderated signals kati ya nodes za hidden layer na output layer, hii simply tuna i equate na sum of the combined moderated signals kati ya nodes za input layer na hidden layer

ni ouput from any node of the hidden layer, hi tuna i equate na

ambayo ni input signal into the network

So based on this symmetry na physical interpretation ya hio equation, tunaona kuwa

ni

Sasa tuziandike hizo equation mbili kwa pamoja

Kwasababu tupo interested kujua direction ya gradient, tunaweza ku drop

completely, kwasababu ni constant inayo scale magnitude ya gradient, sisi hatupo interested na magnitude ya gradient bali its direction

So hii ni final result

Kwa kutumia hizo equations mbili tunaweza ku compute gradient ya error function with respect to any weight in the network, hii ni step muhimu kwa mahesabu ya gradient descent

Tutumie mda huu ku summarize yote tuliyojifunza so far:

The symmetry in neural networks refers to the idea that the method used to calculate the error gradient and update weights in one layer can be similarly applied to other layers due to the network's consistent structure. For example, the process for adjusting weights between the hidden and output layers involves calculating the error (difference between target and actual outputs), the signals entering the output layer, and the outputs from the hidden layer. This same approach can be applied to the input-to-hidden layer by considering the backpropagated error from the hidden layer, the signals entering the hidden layer, and the outputs from the input layer. This symmetry simplifies the training process by allowing the same principles to be reused across different parts of the network.

Next : How to update weights using Gradient Descent

 

[Kuchwizzy]

Part 15 - How to update weights using Gradient Descent​

Kwenye lecture iliyopita, tumeona jinsi gani tunaweza ku compute gradient of the error function with respect to any weight
Kwa maneno mengine tunajua wapi kwenye hii higher dimensional space of error kuna muinuko mkali (steepest slope)
Gradient descent inatutaka tu take step in opposite direction, i.e tu change value of weight in the opposite direction of the gradient

Kama gradient ina move towards positive direction, to move weight in negative direction, na kama gradient ina move towards negative direction to move weight in positive direction

Mathematically, tunachosema ni kwamba thamani mpya ya weight (weight update) tunaipata kwa:

for any weight kati ya hidden layer na output layer

for any weight kati ya input layer na hidden layer

ni Learning rate, kwenye lecture zilizopita tulitumia

ni kitu kilekile, notation tu imebadilika
Tuliona faida ya Learning rate kwenye lectures zilizopita, inatusaidia ku take step kule gradient descent inapotuongoza but partially, ili tu avoid bias ya hio direction.

Kisha tuna rudia hii process mpaka pale tunapo karibia local minima ya error function, kwa maneno mengine ni mpaka pale tutakapo reduce error (tofauti kati ya target value na predicted value)

Hizi ni hatua za Gradient descent algorithm

1. Tunaanza na ku initialize random weights

2. Kwa kila weight, tuna compute its partial derivative with respect to loss or error function, yaani gradient

3. Kisha tuna update value ya weight kwa ku take step in opposite direction of the gradient

4. Tunarudia hatu ya 2 na ya 3 mpaka pale tunapo ridhika na last updated value of weight

Hii ni Pseudocode ya Gradient Descent Algorithm

In simple english

Inaendelea....

 

[Andazi]

Hii ishu ngumu wacha nifanye mengine

 

[Le professel]

Subscribed